Limits of the AP CS Syllabus
-
Most of the information on this page is not actually on your syllabus and can be skipped.
-
However, this page will explain the reasons for the following:
-
Overflow, underflow when using int(which are on your syllabus)and precision problems when using double(which is something worth explaining).
Learning Objectives:
-
Express numbers in binary.
-
Understand the reasons for overflow, underflow when using
int
and precision problems when usingdouble
.
Essential Knowledge:
-
If an expression would evaluate to an
int
value outside of the allowed range, an integer overflow occurs. This could result in an incorrect value within the allowed range.
The Binary System
-
Computers store information(data of all types - numbers, characters, sound, pictures, ...)in binary format i.e. base 2.
-
i.e. 0 or 1
-
Used because computers can only store and understand 2 states:
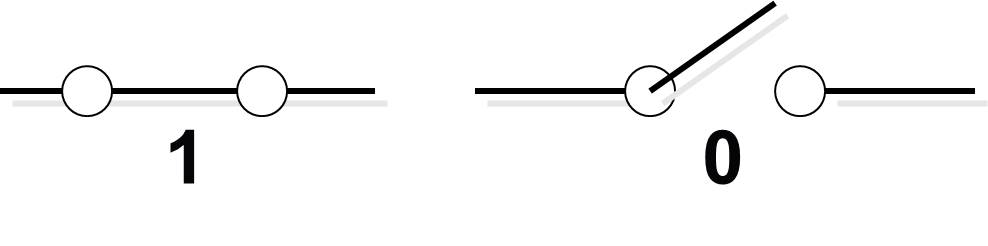
Bits and Bytes
-
A binary digit(1 or 0)is known as a "bit", short for BInary digiT.
-
In modern computers bits are grouped in 8 bit bytes.
Character Set
The symbols that a computer
(software)
can recognise which are represented by binary codes that the computer understands.
Character Representation
-
Over the years different computer designers have used different sets of binary codes for representing characters in a character set.
-
This has led to great difficulty in transferring information from one computer to another.
-
i.e. which binary code represents each character
ASCII (American Standard Code for Information Interchange)
-
Represents each character in a standard character set as a single byte binary code.
-
The standard code form that most PCs use to allow for communication between systems.
-
Usually uses a 7 bit binary code so can store 128 different characters and simple communications protocols.
-
Sufficient for all characters on a standard keyboard plus control codes.
-
Short for character and is used to represent a single character(includes all symbols on a keyboard).
Unicode
-
16 bit code so can store 65536 characters and codes and simple communications protocols.
-
Used to allow coding of languages that do not use Western characters.
ASCII codes
-
The first 32 ASCII codes are used for simple communications protocols and "non-character" keys.
-
e.g. 0000 0110 = ACK - acknowledge and would be sent by a device to acknowledge receipt of data.
-
...
-
0010 0000 = space
-
...
-
...
-
0010 0001 = !
-
...
-
0011 0000 = 0
-
0011 0001 = 1
-
0011 0010 = 2
-
...
-
0100 0001 = A
-
0100 0010 = B
-
...
Representing Characters and Numbers Examples
-
If the "A" key is pressed 1000001 is sent to the Central Processing Unit (CPU).
-
If the 1 key is pressed then 0110001 is sent to the CPU.
-
If the user wants to print "123" the codes for 1, 2 & 3 are sent to the printer.
Binary Arithmetic Rules
-
0 + 0 = 0
-
0 + 1 = 1
-
1 + 0 = 1
-
1 + 1 = 0 (carry 1)
| 1 | |
|---|---|
| + | 1 |
| 1 | 0 |
Please note that our "normal" decimal base 10 system does this "carry & reset" at 10, but binary being base 2, "carries & resets" at 2.
-
1 + 1 + 1 = 1 (carry 1)
| 1 | |
|---|---|
| 1 | |
| + | 1 |
| 1 | 1 |
ASCII Arithmetic
-
ASCII coding is fine for input and output but useless for arithmetic:
| 0 | 00110000 | |||||
|---|---|---|---|---|---|---|
| + | 1 | + | 00110001 | |||
| 1 | 01100001 | i.e. not 00110001 like it ahould be! | ||||
| 01100001 | (carries) |
Decimal or Denary System
-
134 = 100 + 30 + 4
-
Each column is worth 10* as much as the last i.e. base 10(10 fingers!).
| 100 | 10 | 1 |
|---|---|---|
| 1 | 3 | 4 |
Binary Number System
-
134 = 128 + 4 + 2
-
Please click any bit in the converter below to toggle between 0 and 1, and "play" with binary numbers.
| Binary Number | |||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| Denary Number | |||||||
0 |
|||||||
-
= (0 * 128) + (0 * 64) + (0 * 32) + (0 * 16) + (0 * 8) + (0 * 4) + (0 * 2) + (0 * 1)
-
The highest number that can be represented is?
Exploding Dots
-
A "fun" way of thinking about binary numbers is demonstrated in the video below but I personally prefer the more mathematical approach I show after the video.
Denary -> Binary e.g. 117
-
Write the column headings for a byte (8 bits).
-
117 < 128 so put a 0 in the '128' column and move to the next column heading.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0 |
-
117 > 64 so put a 1 in the '64' column, subtract 64 from the denary number being converted to binary (117 - 64 = 53) and move to the next column heading.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 1 |
-
53 > 32 so put a 1 in the '32' column, further subtract 32 from the denary number being converted to binary (53 - 32 = 21) and move to the next column heading.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 |
-
21 > 16 so put a 1 in the '16' column, further subtract 16 from the denary number being converted to binary (21 - 16 = 5) and move to the next column heading.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 |
-
Continue this process until the entire number has been converted (if any bits remain unused they should be 0).
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
Decimal -> Binary Practice
Binary -> Denary e.g. 10110110
-
Put the column headings above the binary number and add up all the columns with a 1 in them.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
-
So 10110110 = 128 + 32 + 16 + 4 + 2 = 182 (denary)
8 bit patterns
-
Because in modern computers bits are grouped in 8 bit bytes numbers in binary format are usually written in 8 bit patterns even if there are unnecessary left leading 0's.
-
e.g. 3(decimal) = 11(binary)
-
But it should be written as 00000011
Binary -> Decimal Practice
Largest number
-
Do you remember the highest number that could be represented with 1 byte(8 bits)?
-
The formula is: 2^(no. of bits) - 1
-
With 2 bytes the largest number that can be represented is?
-
With 3 bytes the largest number that can be represented is?
-
With 4 bytes the largest number that can be represented is?
-
4 bytes is actually what most computer systems use, but do you remember when the "Gangnam Style" song broke youtube's counter? See the video below if you are curious but note I will cover the "sign bit" concept next.
Two's Complement
-
A way to represent negative numbers.
-
Imagine a km clock in a car set at 00000000 kilometres.
-
If the car goes forward one km the reading becomes 00000001.
-
If the meter was turned back one km the reading would be 99999999 km.
-
This could be interpreted as '-1' km.
-
So:
- ...
- 0 0000011 = 3
- 0 0000010 = 2
- 0 0000001 = 1
- 0 0000000 = 0
- 1 1111111 = -1
- 1 1111110 = -2
- 1 1111101 = -3
- Sign Bit
- ...
-
Please click any bit in the converter below to toggle between 0 and 1, and "play" with 2's complement binary numbers.
| Binary Number | |||||||
| -128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| Denary Number | |||||||
0 |
|||||||
-
= (0 * -128) + (0 * 64) + (0 * 32) + (0 * 16) + (0 * 8) + (0 * 4) + (0 * 2) + (0 * 1)
-
Please note that the highest number that can now be represented has been reduced to , but negative numbers can now be represented down to .
Overflow Problem with Two's Complement
-
+102 = 01100110
-
+117 = 01110101
-
102+117 = 219
but
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | |||
|---|---|---|---|---|---|---|---|---|---|---|
| + | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | ||
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | = -37 | ||
| 1 | 1 | 1 | (carries) | |||||||
-
The original numbers are positive but the answer is negative!
-
There has been an overflow from the positive part of the byte to the negative because the answer is larger than the highest number that can be represented with the number of bits allocated.
-
Basically, the number has gone so high that it has "overflowed" into the negative half of 2's complement representation.
-
If you once again consider the analogy of a car km clock and imagine continually turning the clock forward, you would eventually reach the "half way point" and the clock would suddenly switch from representing positive numbers to representing negative numbers instead.
-
Similarily an underflow can occur from the negative part of the byte to the positive when subtraction results in a number lower than the smallest negative number than can be represented with the number of bits allocated.
- e.g. If you try to place 2147483648 in an int (+1 of the maximum positive 2147483647), Java will assign -2147483648 to the int (the lowest negative number).
- Vice versa for underflow.
-
As mentioned at the beginning, the 2 statements above are the only statements that are actually on your syllabus, however I have attempted to explain the reasons for these statements. The rest of the information on this page is for interest only.
-
The only solution to this problem is to increase the number of bits to represent the higher number.
Fixed Point Binary
-
We can extend the binary system to represent real numbers by reserving some bits for the real or fractional part.
-
Note that java actually uses 8 bytes(64 bits)to represent a double so the range is actually more than shown below(however, the basic principles remain the same).
| Binary Number | ||||||||
| Integer | Fraction | |||||||
| -8 | 4 | 2 | 1 | . | 1/2 | 1/4 | 1/8 | 1/16 |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | |
6.75 = 0110.1100
-
Please click any bit in the converter below to toggle between 0 and 1, and "play" with fixed point binary numbers.
| Binary Number | ||||||||
| Integer | Fraction | |||||||
| -8 | 4 | 2 | 1 | . | 1/2 | 1/4 | 1/8 | 1/16 |
|---|---|---|---|---|---|---|---|---|
| Denary Number | ||||||||
0 |
||||||||
-
Please note that the range of numbers that can be represented has been further reduced to to , but fractional numbers can now be represented.
Fixed Point Binary Precision
-
The fractional part can only hold 4 places, any places after the first 4 will be either rounded or truncated, so precision will be lost.
-
This might first appear to be accurate enough for most purposes, however, each binary digit after the point is worth half of the last not 1/10 like in decimal values.
-
110.1 = 6.5
-
110.11 = 6.75
-
We have missed out 6.51 to 6.74!
-
This means accuracy is poor.
Standard Form / Scientific Notation
-
e.g. 1,400,000,000,000dec = 1.4*1012
-
1.4 = mantissa, 12 = exponent
-
Therefore held in two parts:
-
Mantissa
-
Some websites state that this is known more correctly as the Significand and that the Mantissa is the number before the decimal point. However, we will use the term Mantissa for the "whole digit string"(e.g. 1.4 in the example above).
-
Exponent
-
Could be represented: 14 12 if it was understood that the 1st part is the mantissa(with a decimal point after the 1st digit)and 2nd part is the exponent.
Floating Point (Fractional Real Numbers)
-
Basically the binary form of Standard form / Scientific notation described above and it vastly increases the representable range of numbers but not accuracy(this can only achieved by using increasingly more bytes/bits):
-
For simplicity we will use 1 byte for each number, with 8 bits for the mantissa and 8 bits for the exponent.
-
Actually Java
double
uses 8 bytes, with 11 bits for exponent and 52 bits for mantissa(however, the same principles apply regardless of the number of bits used). -
Please click any bit in the converter below to toggle between 0 and 1, and "play" with floating point binary numbers.
-
As well as "playing" try to find the following(the converter below will tell you in the last row if you manage to do so).
-
Highest positive number that can be represented.
-
Lowest positive number that can be represented.
-
Highest negative number that can be represented.
-
Lowest negative number that can be represented.
-
Note: To stop multiple floating point representations of the same number only normalised floating point binary representations are actually considered valid(the 1st 2 bits in the mantissa must be different).
-
e.g. Try representing -1.5 (there are at least 2 different ways but only 1 way is normalised).
Mantissa Exponent Fraction Decimal 0Decimal Number 00* 2 = 0Mantissa Exponent -1 . 1/2 1/4 1/8 1/16 1/32 1/64 1/128 -128 64 32 16 8 4 2 1 Not normalised!
Binary Fractional Precision -
